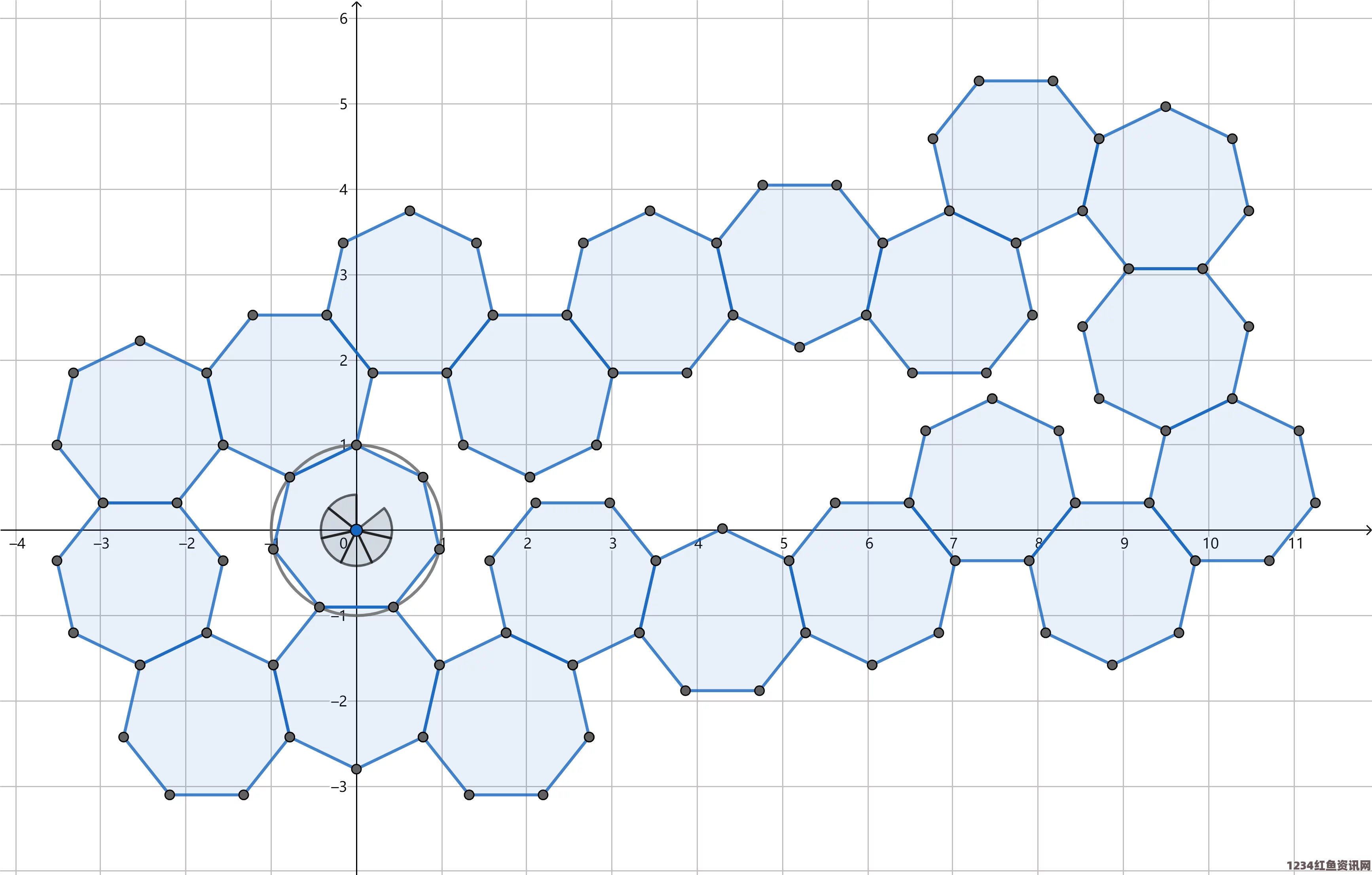
美国数学家突破常规,成功发现一种新型五边形,能够实现无缝密铺平面。这一发现打破了传统几何学的认知,为数学界带来了奇迹。这一成果不仅丰富了平面几何学的理论,也为材料科学、计算机图形学等领域提供了新的思路和方法。这一发现将有望为未来的科学研究和技术创新带来重要影响。
本文导读:
美国数学界传来喜讯,一支顶尖数学研究团队成功发现了一种新型五边形,其能够实现无缝密铺平面,这一发现无疑为几何学领域注入了新的活力,此项成果不仅丰富了平面几何学的理论,也为实际应用提供了更多可能性,我们将详细介绍这一重大发现及其背后的研究故事。
研究背景
无缝密铺平面一直是数学家们追求的梦想,传统的密铺方式主要依赖于三角形、四边形等形状,而五边形的密铺则具有更大的挑战性和复杂性,过去,尽管有许多研究者尝试探索五边形的密铺方式,但进展一直较为缓慢,此次美国数学家的发现,打破了这一僵局。
研究过程
这支研究团队在探索五边形密铺的过程中,采用了先进的计算机技术和数学建模方法,他们首先设计了一种新型五边形,然后通过计算机模拟和实验验证,证明了这种五边形能够实现无缝密铺平面,在研究过程中,团队成员们克服了种种困难,不断尝试、调整和优化设计方案,最终取得了突破性的成果。
研究成果
新型五边形的发现,为平面几何学领域带来了诸多新的可能性,这一成果丰富了平面几何学的理论体系,为几何学的发展注入了新的动力,新型五边形的密铺方式在实际应用中具有广阔的前景,例如在材料科学、建筑设计、艺术创作等领域,这一发现还可能为数学与其他学科的交叉融合提供新的思路和方法。
研究意义
此次新型五边形无缝密铺平面的发现,具有重大的理论和实践意义,在理论方面,这一成果挑战了传统的几何观念,推动了平面几何学的发展,在实践方面,新型五边形的密铺方式为各个领域提供了更多的选择和可能性,有助于推动相关领域的创新和发展。
问答环节:
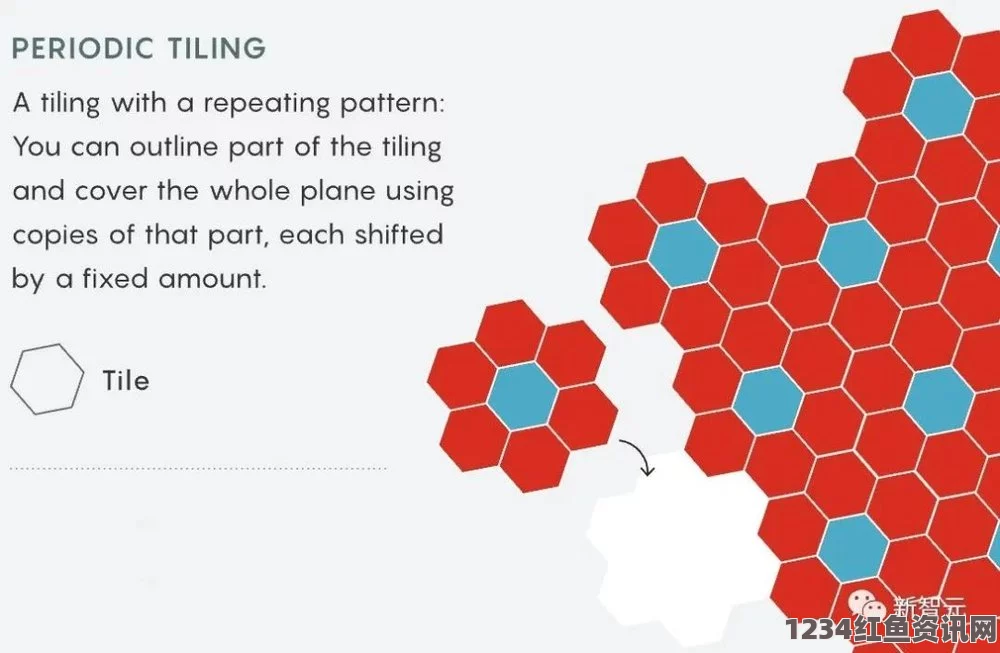
问题一:什么是无缝密铺平面?
答:无缝密铺平面是指将多个几何形状(如多边形)紧密排列在一起,使得整个平面被完全覆盖,且没有任何空隙或重叠,这一发现对于几何学、材料科学、建筑设计等领域具有重要意义。
问题二:为何五边形密铺具有挑战性?
答:五边形密铺具有挑战性主要是因为五边形的角度和边长组合较为复杂,要实现无缝密铺需要满足更为严格的条件,与三角形和四边形的密铺相比,五边形的密铺方式更为多样和复杂。
问题三:新型五边形密铺的应用前景如何?
答:新型五边形密铺的应用前景非常广阔,在材料科学方面,这一成果有助于设计和开发具有独特结构和性能的材料,在建筑设计方面,新型五边形的密铺方式可以为建筑师提供更多的创意和设计灵感,在艺术创作领域,新型五边形密铺也可以为艺术家提供更多的表现手段。
美国数学家发现的这种新型五边形无缝密铺平面的成果,无疑为几何学领域注入了新的活力,具有丰富的理论内涵和广阔的应用前景,我们期待这一成果能够在未来为相关领域带来更多的创新和突破。
